I’m very much enjoying reading Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics by John Derbyshire at the moment. It’s very accessible. It takes time to describe the personalities of the mathematicians, the political and social environments they grew up and worked in. Perhaps more impressively it gives the reader a taste of the personality of various numbers and functions too.
Here’s some categories I’ve clarified my understanding of. A hierarchy of various flavours of numbers:
ℕ - Natural Numbers
Some examples: One; Two; Five; Seven-Hundred
These are numbers used to count things, they are whole numbers from one upwards.
1, 2, 3, 4, 5...
You can always add with natural numbers: 2 + 3 = 5
You can’t subtract a larger number from a smaller number with natural numbers.
All the same lets try: Place 3 biscuits in front of you; now eat 5 biscuits.
What happens? You run out of biscuits before you’ve managed to get to 5 eaten.
And this is the constraint of natural numbers.
3 - 5 = nonsense.
Zero is a disputed topic, zero isn’t a natural number, but some people think it might be. I most certainly am not qualified to offer judgement and so advise nodding and smiling should anyone decide to argue this point.
ℤ - Integers
Take any natural number, poke a minus sign before it and you have a negative number.
-5, -4, -3, -2, -1
The set of integers includes all natural numbers, and an equivalent set of negative numbers which are the same numbers with a minus sign in front of them.
Zero is definitely in the set of integers (whether or not it’s a natural number).
0
If you want to be explicit that you have a positive number, you can display
a natural number as an integer by putting a plus sign in front of it. Most of
the time this isn’t necessary as the + is implicit, all the same here’s what
it looks like:
+1, +2, +3, +4
With integers it’s now possible to subtract a larger number from a smaller one. This time grab just 1 biscuit 🍪 from the tin, a pen and a nice large piece of paper.
I used to think the number line a little simplistic, but I’ve now grown fond of it, draw yourself a number line like this on the large sheet of paper:
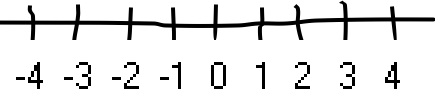
We’re going to try 3 - 5 = ? again, so place the biscuit on the number 3.
Now slide the biscuit to the left, each time you pass a number mark, count up
to five. All being well the biscuit should land on -2. If it didn’t, don’t
worry, in the technology business, we call that an “off-by-one error”, simply
eat the biscuit and try again.
Hopefully the biscuits didn’t run out before we worked out that 3 - 5 = -2.
Well done, pat yourself on the back have a biscuit, you’re now familiar with
integers.
ℚ - Rational Numbers
So, we’re at the end of the packet, there’s only one biscuit left, and two of us here wishing to eat the biscuit, what can we do? Well, with integers, we have the following options:
- One of us courteously offers the biscuit to the other
- Fight to the death, winner claims the biscuit
To reach a fairer solution we can use fractions. In this case we can break the
biscuit into two halves. The mathematical term for break in this context is
divide. 1 ÷ 2 = ½ say “one (biscuit) divided by two (pieces) equals a half
(each)”
To write a half we have a horizontal or diagonal line with a 1 balancing on top and a 2 underneath. To create a fraction we take any two integers and arrange them this way with one on top and the other underneath.
Here’s a 3 balancing on a 5 ⅗ say “three fifths” try to break a cookie like
this if the other person isn’t looking and keep the bigger bit.
You can even write integers as fractions should the need arise, to do so: balance your integer on top of a 1.
50⁄1
This works because any number divided by 1 equals itself. One biscuit divided among 1 person equals one whole biscuit.
Getting back to rational numbers, these are any of the fractions and any of the integers.
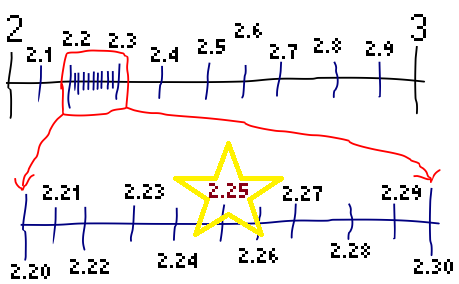
You can write fractions as decimals too, so ½ = 0.5 or ¼ = 0.25 you can use
the trusty number line again to understand these: to do so, imagine splitting
the space between two numbers into 10 even gaps. You count along those gaps to
find the first digit after the decimal place. You can then further subdivide
those divisions and that’s the following decimal place.
Here’s the number 2.25 AKA “two and a quarter” illustrated this way:
All the integers can be re-written as rational numbers by adding a decimal point and as many zeroes as you care to add.
5 = 5.000
ℝ - Real Numbers
Well done for sticking it out this far! Things start to get a little strange from here on. I’d like to introduce you next to irrational numbers.
An irrational number is one which has the following curious properties:
- However many decimal places you write it down to, there are always more
- It can’t be expressed as a fraction
The number for ⅓ say “a third” is an interesting rational number: it can be expressed as a fraction, but if you attempt to write it out as a decimal number you get 0.333 followed by a never ending set of threes.
An interesting quality of this and any other rational number is that it can either be written down in full, or if it can’t then you’ll get a repeated sequence of numbers (like the 3s in the above example).
So back to irrational numbers: The most famous celebrity irrational number is π say “pi”. This has a value of approximately 3.14159 plus a never ending set of numbers, which unlike the 3s in a third, don’t repeat.
Typically, the particularly useful irrational numbers have been given a letter such as e for Euler’s (say “oiler”) constant, or as in π a greek letter.
ℂ - Complex Numbers
This magical set of numbers includes every single one of the types of numbers described so far and one extra: Imaginary Numbers.
Unfortunately these aren’t mumbo jumbo numbers with silly names like “eleventy seven” or “noughty third” although that would be fun.
To square a number is to times it by itself. So two squared, written: 2² is
two times two, which is 4. Likewise 3² = 3 x 3 = 9.
To reverse that operation you can use a square-root. The “square root of nine”
means “what squared equals nine” this is written √9 = 3. Similarly √4 = 2
In much the same way you are not able to express some subtractions with natural
numbers, should you wish to find the square root of a negative number, it
cannot be expressed with real numbers. Instead we have to use Imaginary
Numbers. To do that, we do a trick: we say that i = √-1 that’s it, the whole
trick!
A Complex Number is one which has a real part and an imaginary part. For
example 5 + 3i where 5 is the real part and 3i is the imaginary part.
Our old friend the number line is useful here too, though to express complex numbers needs another axis:

On this chart, all the numbers discussed so far prior to complex numbers live
on the real axis, where the imaginary value is 0i. You can use this trick to
express a real number as a complex number: add 0i like this: 25 = 25 + 0i
I think that’s super cool, you can turn any boring old counting number into a
complex number, like magic! I just boiled the kettle and made 2 + 0i cups of
tea!
Why might you wish to care about complex numbers? Reason is, you might find working with complex numbers to solve a problem is easier.
Summary
I hope you enjoyed my little tour of number types!
In case you were wondering the hollowed out letter in each of the headings
is the official letter representing each of the number types:
ℕ < ℤ < ℚ < ℝ < ℂ. The mnemonic recommended in the book is: Nine Zulu Queens
Ruled China.